Minimización de estados en un AF

Un autómata finito (AF) o máquina de estado finito es un modelo computacional que realiza cómputos en forma automática sobre una entrada para producir una salida.

Este modelo está conformado por un alfabeto, un conjunto de estados y un conjunto de transiciones entre dichos estados. Su funcionamiento se basa en una función de transición, que recibe a partir de un estado inicial una cadena de caracteres pertenecientes al alfabeto (la entrada), y que va leyendo dicha cadena a medida que el autómata se desplaza de un estado a otro, para finalmente detenerse en un estado final o de aceptación, que representa la salida.

La finalidad de los autómatas finitos es la de reconocer lenguajes regulares, que corresponden a los lenguajes formales más simples según la Jerarquía de Chomsky.

Definición formal Formalmente:

E: alfabeto de entrada.

Q: conjunto de estados; es conjunto finito no vacío.

f: función de transición. f(p,a)=q

q0 : (perteneciente a Q) estado inicial.

F : (perteneciente a Q) conjunto de estados finales o de aceptación.

En el comienzo del proceso de reconocimiento de una cadena de entrada, el autómata finito se encuentra en el estado inicial y a medida que procesa cada símbolo de la cadena va cambiando de estado de acuerdo a lo determinado por la función de transición. 

Cuando se ha procesado el último de los símbolos de la cadena de entrada, el autómata 

CLASIFICACIÓN DE AF LOS AUTÓMATAS SE PUEDEN CLASIFICAR EN:

· Deterministas; Cada combinación (estado, símbolo de entrada) produce un solo estado.

· No Deterministas; Cada combinación (estado, símbolo de entrada) produce varios estados y además son posibles las transiciones con λ.

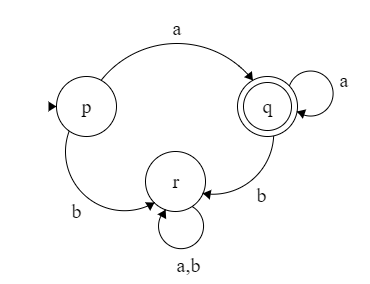
Los autómatas se pueden representar mediante tablas de transición o diagramas de transición.